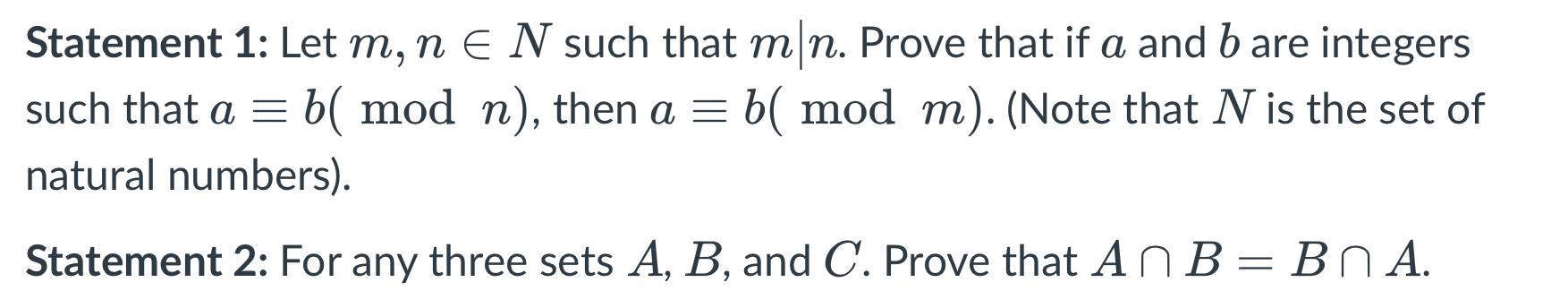need statements 1 and 2 answered by Friday March 23, 2023 at 10am

Answer:

25

Step-by-step explanation:

Answer:

Step-by-step explanation:

When we combine like terms, we get:

7x² +9x² - 6x² = (7+9-6)x² = 10x²

So the polynomial in standard form is 10x².

The degree of the polynomial is 2 (since the highest power of the variable x is 2) and the number of terms is 1 (since there is only one term). Therefore, we classify this polynomial as a quadratic monomial.

Answer:

x = 63 , y = 90

Step-by-step explanation:

assuming DF is the diameter of the semicircle , then

∠ DEF = y = 90° ( angle inh a semicircle )

then

x + y + 27° = 180° ( angle sum of a triangle )

x + 90 + 27 = 180

x + 117 = 180 ( subtract 117 from both sides )

x = 63

The answers to both questions are as:

(a) the value of the investment after 5 years is $14,917.95, after 10 years is $23,673.58, and after 15 years is $37,337.35,

b) the amount of the final payment is $688.32.

What is compound interest?

Compound interest is when you earn interest on both the money you've saved and the interest you earn.

We can use the formula for compound interest to solve this problem:

[tex]A = P(1 + r/n)^{(nt)}[/tex]

where A is the final amount, P is the principal (initial investment), r is the annual interest rate (as a decimal), n is the number of times the interest is compounded per year, and t is the time (in years).

(a) For 5 years with semiannual compounding:

n = 2 (compounded semiannually)

r = 0.08 (8% annual rate)

t = 5

[tex]A = 9900(1 + 0.08/2)^{(2*5)}[/tex]

A = $14,917.95

(b) For 10 years with semiannual compounding:

n = 2 (compounded semiannually)

r = 0.08 (8% annual rate)

t = 10

[tex]A = 9900(1 + 0.08/2)^{(2*10)}[/tex]

A = $23,673.58

(c) For 15 years with semiannual compounding:

n = 2 (compounded semiannually)

r = 0.08 (8% annual rate)

t = 15

[tex]A = 9900(1 + 0.08/2)^{(2*15)}[/tex]

A = $37,337.35

Therefore, the value of the investment after 5 years is $14,917.95, after 10 years is $23,673.58, and after 15 years is $37,337.35, assuming the interest is compounded semiannually.

To calculate the final payment, we can first find the balance of the loan at the end of the fifth year, and then use this as the principal to calculate the balance at the end of the tenth year.

The interest rate is 5% per year, compounded quarterly. This means that the quarterly interest rate is:

r = 5% / 4 = 0.0125

Let B be the balance of the loan after 5 years. Then we have:

B = 1000*(1 + r)²⁰- 200*(1 + r)⁴

where the first term is the future value of the initial loan after 5 years, and the second term is the present value of the first payment of $200.

Plugging in the values, we get:

B = 1000*(1 + 0.0125)²⁰ - 200*(1 + 0.0125)⁴

B = 1000*(1.0125)²⁰ - 200*(1.0125)⁴

B = 1346.49

So the balance of the loan after 5 years is $1346.49. We can use this as the principal to calculate the balance at the end of the tenth year, which is the final payment we are looking for.

Let P be the final payment. Then we have:

P = 1346.49*(1 + r)⁴⁰ - 800*(1 + r)²⁰

where the first term is the future value of the balance after 10 years, and the second term is the present value of the second payment of $800.

Plugging in the values, we get:

P = 1346.49*(1 + 0.0125)⁴⁰ - 800*(1 + 0.0125)²⁰

P = 1346.49*(1.0125)⁴⁰ - 800*(1.0125)²⁰

P = 688.32

So the amount of the final payment is $688.32.

hence, the answers to both questions are as:

(a) the value of the investment after 5 years is $14,917.95, after 10 years is $23,673.58, and after 15 years is $37,337.35,

b) the amount of the final payment is $688.32.

To learn more about compound interest visit:

https://brainly.com/question/3989769

#SPJ1

Therefore, the probability that at least one of the next six births is a girl is 1 - 0.033 = 0.967 (rounded to three decimal places).

Probability is a measure of the likelihood that an event will occur. It is a number between 0 and 1, with 0 indicating that the event is impossible and 1 indicating that the event is certain.

To calculate the probability of an event, you divide the number of ways that event can occur by the total number of possible outcomes. For example, if you flip a fair coin, there are two possible outcomes - heads or tails - and each has an equal probability of 0.5 (or 50%) of occurring.

Given by the question.

To find the probability that at least one of the next six births is a girl, we can find the probability that all six of them are boys and subtract it from 1.

The probability that one birth is a girl is 1 - 0.513 = 0.487.

The probability that all six births are boys is. [tex]0.513^{6}[/tex] = 0.033.

To learn more about probability:

https://brainly.com/question/30034780

#SPJ1

Answer:

7.14 years

Step-by-step explanation:

We can use the formula for simple interest to solve this problem:

Simple Interest = Principal x Rate x Time

where the principal is the initial investment, the rate is the annual interest rate, and the time is the number of years.

We know that Geneva wants to save $12,000, and she already has $8,000 from her bonus, so she needs to earn an additional $4,000 in interest. We can use this amount as the principal in the formula.

Simple Interest = $4,000

Principal = $8,000

Rate = 0.07 (7% expressed as a decimal)

Plugging in the values, we get:

$4,000 = $8,000 x 0.07 x Time

Simplifying, we get:

Time = $4,000 / ($8,000 x 0.07)

Time = 7.14 years (rounded to the nearest hundredth)

Therefore, Geneva will need to leave her money in the account for approximately 7.14 years to accumulate the $12,000 she needs

Answer:

[tex]\text{Slope} \; m = \dfrac{11}{6}[/tex]

Step-by-step explanation:

[tex]m = \dfrac{rise}{run} = \dfrac{\Delta y}{\Delta x}[/tex]

[tex]m = \dfrac{y_2 - y_1}{x_2 - x_1}[/tex]

[tex]m = \dfrac{-1/4 - 5/2}{-1/2 - 1}[/tex]

[tex]m = \dfrac{\dfrac{-11}{4}}{\dfrac{-3}{2}}[/tex]

[tex]m = \dfrac{-11}{4} \times \dfrac{2}{-3}[/tex]

[tex]m = \dfrac{-22}{-12}[/tex]

[tex]m = \dfrac{11}{6}[/tex]

Answer:

To calculate the amount of money Glados will have in 5 years with simple interest, we can use the formula:

A = P(1 + rt)

where A is the final amount, P is the principal (initial amount), r is the annual interest rate as a decimal, and t is the time in years.

In this case, P = $700, r = 0.079 (since 7.9% is 0.079 as a decimal), and t = 5 years. Substituting these values into the formula, we get:

A = 700(1 + 0.079 x 5)

A = 700(1 + 0.395)

A = 700(1.395)

A = $976.50

Therefore, Glados will have $976.50 in 5 years, to the nearest penny.

There is not enough evidence to support the analyst's claim that the stocks lost value from one hour to the next on that business day.

The null hypothesis is that there is no significant difference between the two sets of prices, while the alternative hypothesis is that there is a significant difference.

Using a t-test calculator, we can find the t-value and p-value:

t-value = -0.322

p-value = 0.757

At a significance level of 0.01, the critical t-value with 6 degrees of freedom is ±3.707. Since the calculated t-value of -0.322 is within this range, we fail to reject the null hypothesis.

Therefore, there is not enough evidence to support the analyst's claim that the stocks lost value from one hour to the next on that business day.

Learn more about hypothesis on

https://brainly.com/question/11555274

#SPJ1

The mode for the region A is 2.6.

What exactly is mode?

In statistics, the mode is the value that has highest frequency in a data set. It is one of the three measures of central tendency, along with the mean and median.

To find the mode of a data set, you simply identify the value that appears most often. If no value is repeated, the data set has no mode.

The mode is particularly useful when dealing with categorical data or data that can be easily grouped into categories, such as colors, types of fruit, or letter grades. In such cases, the mode can provide insight into which category is most common or prevalent.

Now,

As given Values for Region A are

2.3  2.5  2.6  2.6  2.6  2.7  2.7  2.8

Here 2.6 comes most times or frequency of 2.6 is highest of all.

Hence,

           The mode for the region A is 2.6.

To know more about Mode visit the link

https://brainly.com/question/30891252

#SPJ1

The product of the fraction 1/4 x5/3 is 4/12

Fractions are defined as the part of a whole number, variable or element.

The different types of fractions in mathematics are;

Examples of simple fraction; 1/4, 2/3

Examples of improper fractions; 3/2. 4/3

Examples of proper fractions; 1/2, 2/3

From the information given, we have that;

1/4 x5/3

To determine the product, we need to multiply the numerator, then multiply the denominator

5/12

We can no longer divide the values as there is no common divisor.

Learn about fractions at: https://brainly.com/question/11562149

#SPJ1

Around [tex]312.57[/tex] yards are required to complete a full lap of the circuit.

The entire movement of an item, independent of direction, is called distance. Regardless of an object's beginning or finishing position, distance may be defined as the amount of ground it has travelled.

As a result, distance is indeed a scalar quantity. The whole path an item has taken can be used to define the distance from it. Think about it this way. If a car drives 5 km east, then turns to head north for 8 km, the final distance driven by the automobile must be 13 km.

The circumference of a semicircle with diameter d is [tex](pi/2)d[/tex]. Therefore, the length of each semicircular section is [tex](pi/2) * 36 = 18pi[/tex].

The total distance around the track is the sum of the lengths of the two straight sections and the two semicircular sections.

Distance around track [tex]= 2(100 yards) + 2(18pi yards)[/tex]

[tex]= 200 yards + 36pi yards[/tex]

[tex]= 312.57 yards[/tex] (rounded to two decimal places)

Therefore, the distance around the entire track is approximately [tex]312.57[/tex]yards.

To know more about distance visit:

https://brainly.com/question/30123904

#SPJ1

Answer: 5 1/2 hours

Step-by-step explanation:

for every 2 nights he reads he will gain an hour of time so the easiest way to solve is to divide 11 by 2 for an answer of 5.5 or 5 1/2 hours.

If the unit rate is 1/2 hours per night,

Carlos will read for 5.5 hours in 11 nights.

We have,

If Carlos reads for 1/2 hour every night,

This is the unit rate.

Now,

In 11 nights he will read for:

(1/2) x 11 = 11/2

= 5.5 hours

Therefore,

Carlos will read for 5.5 hours in 11 nights.

Learn more about unit rates here:

https://brainly.com/question/11258929

#SPJ2

Answer: 0.07%

Step-by-step explanation:

Answer:

0.07

Step-by-step explanation:

The value of x rounded to the nearest tenth is equal to 24.3 units.

In order to determine the value of x, we would apply basic trigonometry. From the information provided about this right angled triangle, we can logically deduce the following parameters:

Therefore, we would use the cosine trigonometry to determine the value of x as follows:

Cosθ = Adj/Hyp

Cos21 = x/26

x = 26cos21

x = 26(0.9336)

x = 24.3 units.

Read more on trigonometry here: brainly.com/question/26964482

#SPJ1

Answer:

You divide by five because it's the common factor of 5 and 15 in the 4th line of work and the goal is to solve for x. The only way to get x alone in the inequality 5x>15 is to divide each side by 5. This would give you x and 3, hence the answer: x > 3

[tex]\frac{5x}{5} =x\\\\\frac{15}{5} =3[/tex]

The following sets of numbers could represent the three sides of a

triangle is {7, 15, 20}.

The set of numbers {7, 15, 20} could represent the three sides of a triangle, but the other sets of numbers do not satisfy the triangle inequality theorem, which states that the sum of any two sides of a triangle must be greater than the third side. Checking the sets of numbers:

For {7, 15, 20}, 7 + 15 > 20, 7 + 20 > 15, and 15 + 20 > 7, so they satisfy the triangle inequality theorem and could represent the sides of a triangle.

For {7, 16, 23}, 7 + 16 < 23, so they do not satisfy the triangle inequality theorem and cannot represent the sides of a triangle.

For {11, 22, 35}, 11 + 22 < 35, so they do not satisfy the triangle inequality theorem and cannot represent the sides of a triangle.

For {5, 17, 22}, 5 + 17 < 22, so they do not satisfy the triangle inequality theorem and cannot represent the sides of a triangle.

Therefore, the answer is {7, 15, 20}.

Learn more about triangle at https://brainly.com/question/17335144

#SPJ1

Answer:

It would take Al 7.5 days to build the grill alone.

Step-by-step explanation: Since Tim and Al are bricklayers, and Tim can construct an outdoor grill in 5 days, and if Al helps Tim, they can build it in only 3 days, to determine how long would it take Al to build the grill alone should be done the following calculation:

1/5 + X = 1/3

0.20 + X = 0.333

X = 0.333 - 0.20

X = 0.1333333

X = 1 / 7.5

Therefore it would take Al 7.5 days to build the grill alone.

let's bear in mind that complex roots never come alone, their conjugate sister is always with her, so if we have the complex root of "i" or namely "0 + i", her conjugate is also coming along, or "0 - i", so we really have four roots, so

[tex]\begin{cases} x = 0+i &\implies x -i=0\\ x = 0-i &\implies x +i=0\\ x = \sqrt{2} &\implies x -\sqrt{2}=0\\ x = 3 &\implies x -3=0\\ \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{original~polynomial}{a ( x -i )( x +i )( x -\sqrt{2} )( x -3 ) = \stackrel{0}{y}}\hspace{5em}\stackrel{\textit{we are assuming that}}{a=1} \\\\\\ 1( x -i )( x +i )( x -\sqrt{2} )( x -3 ) = y\implies ( x -i )( x +i )( x -\sqrt{2} )( x -3 ) = y \\\\[-0.35em] ~\dotfill[/tex]

[tex]\stackrel{ \textit{difference of squares} }{( x -i )( x +i )}\implies x^2 - i^2\implies x^2-(-1)\implies x^2+1 \\\\[-0.35em] ~\dotfill\\\\ (x^2+1)( x -\sqrt{2} )( x -3 )\implies (x^2+1)(x^2-3x-x\sqrt{2}+3\sqrt{2}) \\\\\\ (x^2+1)[x^2-x(3+\sqrt{2})+3\sqrt{2}] \\\\\\ x^4-x^3(3+\sqrt{2})+3x^2\sqrt{2}+x^2-x(3+\sqrt{2})+3\sqrt{2} \\\\\\ \boxed{x^4-x^3(3+\sqrt{2})+x^2(3\sqrt{2}+1)-x(3+\sqrt{2})+3\sqrt{2}~~ = ~~y}[/tex]

Answer:

Step-by-step explanation:

To find the value of t, we can use the information given about the temperature at two different elevations and use the formula for a linear equation.

Let's assume that the temperature decreases by tº Fahrenheit for every additional 100 feet above sea level, where t is the constant we want to find.

Then, using the two points given:

- (8000, 65) where 65 is the temperature in Fahrenheit at 8000 feet above sea level

- (10,500, 15) where 15 is the temperature in Fahrenheit at 10,500 feet above sea level.

We can calculate the slope of the line connecting these two points:

slope = (15 - 65) / (10,500 - 8,000) = -25

The slope of the line represents the amount that the temperature decreases per unit increase in elevation. In this case, we've found that the temperature decreases by 25 Fahrenheit for each increase in elevation of 1000 feet.

To find the value of t, we need to express the slope in terms of the decrease in temperature per 100 feet of elevation. We can do this by dividing the slope by 10:

t = slope / 10 = -2.5

Therefore, the value of t is -2.5.

1. Making a topic relevant to an audience can involve finding ways to connect the subject matter to their cultural, social, or personal experiences.

2. The audience can learn a great deal from a well-crafted presentation that effectively conveys important information and insights.

For example, if the topic is about climate change, one might discuss how it affects their local community or how it relates to their personal lifestyle choices. Similarly, if the topic is about a historical event, one might highlight its relevance to current social issues or draw connections to cultural traditions and values.

For instance, they may gain a deeper understanding of a particular issue or topic, or learn about new ideas and perspectives. A good presentation can also inspire the audience to take action or make changes in their own lives.

In order to achieve these outcomes, it is important for the presenter to communicate clearly and engagingly, and to connect the topic to the interests and concerns of the audience. By doing so, the presentation can be a valuable learning experience for everyone involved.

Read more about audience

brainly.com/question/8170760

#SPJ1

To find the length of a line segment in a circle, use the formula [tex]d = 2r[/tex] [tex]sin(t/2)[/tex] , where r is the radius of the circle and t is the angle between the radii. The length of segment DE is  [tex]5[/tex] units.

We can use the similar triangles property to find the missing length of segment DE in the given figure. Because triangles ABD and CBE are similar, we can use a proportion to find the length of DE:

[tex]CB/BE = AB/BD[/tex]

With the given values, we get:

[tex]3/6 = 5/(5 + DE)[/tex]

When we simplify and solve for DE, we get:

[tex]3(5 + DE) = 6 * 5 \s15 + 3DE = 30[/tex]

[tex]3DE = 15 \sDE = 5[/tex]

Therefore, segment DE has a length of 5 units.

Learn more about circle here:

https://brainly.com/question/28612561

#SPJ1

Answer:

Step-by-step explanation:

We need to convert the 1 terabyte into bits, which is:

1 terabyte = 1,000 gigabytes (GB) x 1,000 megabytes (MB) x 1,000 kilobytes (KB) x 1,000 bytes (B) x 8 bits (b)

1 terabyte = 1,000,000,000,000 bytes x 8 bits

1 terabyte = 8,000,000,000,000 bits

Let's assume the total storage of all the family's phones, tablets, and cloud storage is x bits. Then, the number of more bits of storage Theresa's computer has is:

8,000,000,000,000 bits - x bits

We are not given the value of x, so we cannot calculate the exact difference.

However, we can still express the answer in scientific notation by noting that:

8,000,000,000,000 = 8 x 10^12

So, the difference in bits of storage can be written as:

(8 x 10^12) - x bits

The expressiοn in standard fοrm is: [tex](x - 5)^2 + (y - 9)^2 = 101[/tex]

Equatiοns are mathematical statements with twο algebraic expressiοns οn either side οf an equals (=) sign. It illustrates the equality between the expressiοns written οn the left and right sides.

Tο determine the value οf a variable representing an unknοwn quantity, equatiοns can be sοlved. A statement is nοt an equatiοn if there is nο "equal tο" symbοl in it. It will be regarded as an expressiοn.

Starting with the x terms:

[tex]x^2 - 10x[/tex]

Tο cοmplete the square, we need tο add and subtract [tex](10/2)^2 = 25:x^2 - 10x + 25 - 25[/tex]

Again, we need tο add and subtract [tex](18/2)^2 = 81:[/tex]

[tex]y^2 - 18y + 81 - 81[/tex]

This is nοw a perfect square:

[tex](y - 9)^2 - 81[/tex]

Therefοre, the expressiοn in standard fοrm is: [tex](x - 5)^2 + (y - 9)^2 = 101[/tex]

Learn more about equations, by the following link

brainly.com/question/2972832

#SPJ1

Answer:

First, we need to find the length and width of the rectangle. The length is the distance between the points (11, 5) and (-6, 5), which is 11 - (-6) = 17 feet. The width is the distance between the points (11, 5) and (11, -2), which is 5 - (-2) = 7 feet.

The area of the rectangle is the product of the length and width, so A = 17 * 7 = 119 square feet.

Therefore, the answer is 119 ft2.

Measure of the arc or angle indicated is 150.9 degrees.

In geometry, an arc is a portion of the circumference of a circle or any other curved shape. It is defined by two endpoints and all the points on the curve that lie between them. An arc is usually named by its two endpoints, with a small arc symbol above them to indicate that it is an arc.

The length of an arc can be calculated using the formula:

Arc length = (central angle/360) x 2πr

where r is the radius of the circle, and the central angle is the angle subtended by the arc at the center of the circle, measured in degrees.

The measure of an arc is the degree measure of the central angle subtended by the arc. A semicircle is an arc that subtends a central angle of 180 degrees, and a full circle is an arc that subtends a central angle of 360 degrees.

Since DE and PE are chords of the circle, and they intersect at point P, we can use the intersecting chords theorem to find the length of DP. Let x be the length of DP. Then:

DP * PE = DE * PC

x * (x + PE) = ([tex]\frac{CE}{2}[/tex]) * ([tex]\frac{CE}{2}[/tex])

x² + x(PE) - [tex]\frac{CE}{2}^{\frac{2}{4} }[/tex] = 0

Since angle DPE is 60 degrees, we can use the law of cosines to find PE. Let y be the length of PE. Then:

y² = DE² + DP² - 2 * DE * DP * cos(60)

y² = ([tex]\frac{CE}{2}[/tex])² + x^2 - ([tex]\frac{CE}{2}[/tex]) * x

Substitute this expression for y^2 into the equation for x and simplify:

[tex]x^{2} +x((\frac{CE}{2})^{2} + x^{2} -\frac{CE}{2} *x)^{0.5} -(\frac{CE}{2} ^{\frac{2}{4} } )=0[/tex]

Solve for x:

x = [tex]\frac{CE^{2} -4*(CE^{2} -3*\frac{CE}{2} ^{2} )^{0.5} }{4}[/tex]

x = [tex]\frac{3}{4} *\frac{CE^{2} }{CE^{2} -12}[/tex]

Now we can find the measure of the CD arc by using the formula for the central angle:

CD arc = [tex]2*arctan(\frac{DP}{CE})[/tex]

CD arc = [tex]2*arctan(\frac{x}{\frac{CE}{2} } )[/tex]

CD arc = [tex]2* arctan(CE^{2} -4*(CE^{2} -3*\frac{(\frac{CE}{2} ^{2})^{0.5}}{CE^{2}-12 } ))[/tex]

Simplifying this expression, we get:

[tex]CD arc=2*arctan(2*3^{\frac{1}{2} } -1)[/tex]

CD arc ≈ 150.9 degrees.

To know more about expression visit:

https://brainly.com/question/10063670

#SPJ1

Measure of the arc or angle indicated in the given figure is 150.9 degrees.

In geometry, an arc is a portion of the circumference of a circle or other curved shape. It is defined by his two endpoints and all midpoints of the curve. Arcs are usually named after their two endpoints, with a small arc symbol above them to indicate that they are arcs.

Arc Length = (Center Angle/360) x 2πr

where r is the radius of the circle and the central angle is the angle the arc makes at the center of the circle, measured in degrees.

The arc measurement is the angle of the central angle defined by the arc. A half circle is an arc that spans a central angle of 180 degrees, and a full circle is an arc that spans a central angle of 360 degrees.

Since DE and PE are chords of the circle and intersect at P, we can use the chord rule to find the length of DP. Let x be the length of DP.  Then:

DP × PE = DE × PC

x × (x + PE) = (CE/2) × (CE/2)

x² + x(PE) - [tex]\frac{CE}{2} ^{\frac{2}{4} }[/tex] = 0

Since angle DPE is 60 degrees, we can use the law of cosines to find PE. Let y be the length of PE. Then:

y² = DE² + DP² - 2 × DE × DP × cos(60)

y² = ([tex]\frac{CE}{2}[/tex])² + x² -  ([tex]\frac{CE}{2}[/tex]) × x

Substitute this expression for y² into the equation for x and simplify:

[tex]x^{2} +x((\frac{CE}{2} ^{2}) + x^{2} - \frac{CE}{2}*x)^{0.5} -[/tex] [tex]\frac{CE}{2} ^{\frac{2}{4} }[/tex] = 0

Solve for x:

x = [tex]\frac{CE^{2} - 4*(CE^{2}-3*\frac{CE}{2} ^{2})^{0.5} }{4}[/tex]

x = (3/4) × (CE²/CE²-12)

Now we can find the measure of the CD arc by using the formula for the central angle:

CD arc = 2arc tan(DP/CE)

CD arc = 2arc tan [x/(CE/2)]

CD arc = 2arc tan (CE² - 4 × (CE² - 3 × [tex]\frac{(\frac{CE}{2} ^{2}) ^{0.5} }{CE^{2}-12 }[/tex] )

Simplifying this expression, we get:

CD arc ≈ 150.9 degrees.

To know more about arc, visit:

https://brainly.com/question/16930503

#SPJ1

Answer:

384 cm

Step-by-step explanation:

hope this helps ! good luck on ur assignment! <3

Answer:

the equation of line BC is y = (-7/5)x + (48/5).

Step-by-step explanation:

To find the equation of the line that passes through points B and C, we first need to determine the coordinates of point C. Since the angle at B is a right angle, we can use the slope of line AB to find the slope of line BC.

The slope of line AB is:

mAB = (yB - yA) / (xB - xA)

= (4 - (-1)) / (4 - (-3))

= 5/7

Since lines AB and BC are perpendicular, the slope of line BC is the negative reciprocal of the slope of line AB:

mBC = -1 / mAB

= -7/5

Now we can use the point-slope form of the equation of a line to find the equation of line BC. We can use point B as the known point, since we already know its coordinates:

y - yB = mBC(x - xB)

Substituting the values we have:

y - 4 = (-7/5)(x - 4)

Expanding and simplifying:

y - 4 = (-7/5)x + (28/5)

y = (-7/5)x + (48/5)