Answers
Answer:
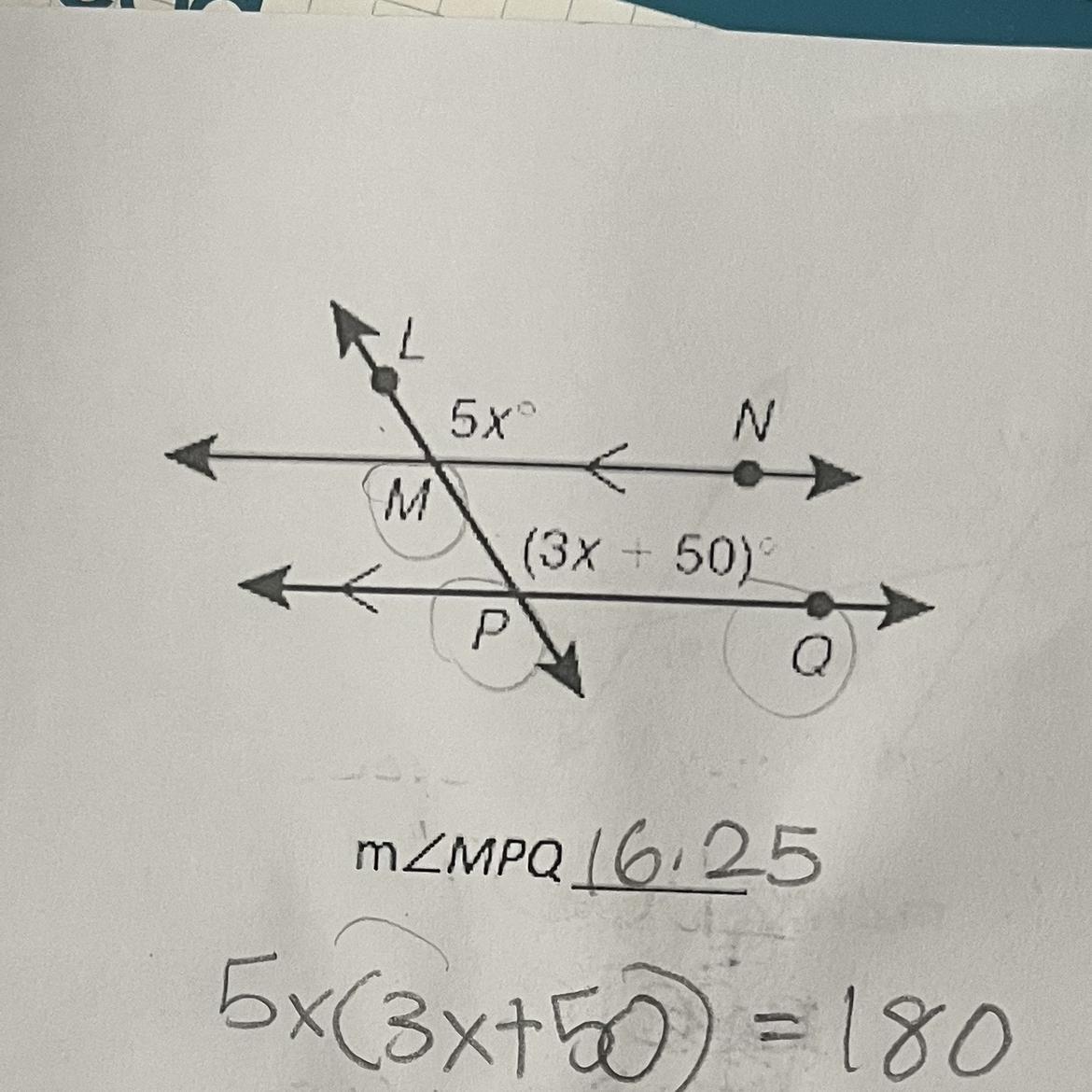
measure of angle MPQ is 125
Step-by-step explanation:
1) Corresponding angles are congruent
5x=3x+50
2x=50
x=25
2) Substitute back into the equation
3(25)+50 = 125
Related Questions
When it comes to the sale of products such as pet food, the veterinary practice is at an advantage over feed stores and grocery stores because
Answers
When it comes to the sale of products such as pet food, the veterinary practice is at an advantage over feed stores and grocery stores because they have better knowledge and understanding about the pet food, and they have established trust with their customers.
What is pet food?
Pet food is a nutrient-rich food specially designed for domestic animals, like dogs, cats, and other pets. It is made from various animal and plant-based sources, such as beef, fish, and corn. Since pet food is designed to meet the nutritional needs of the pets, it must be balanced and complete to provide them with the necessary nutrients they need to be healthy and active.
Why veterinary practice is at an advantage over feed stores and grocery stores?Veterinarians are at an advantage over feed stores and grocery stores when it comes to the sale of pet food because they have the knowledge and expertise about the pet food. They are aware of the specific nutritional requirements of the pets and the various pet food brands available in the market. They can provide advice and recommendations to pet owners on what type of pet food is best suited for their pets based on their age, breed, and health conditions.
Moreover, veterinary practices have established trust with their customers. When customers know they can rely on a particular veterinary practice for quality products and trustworthy advice, they are more likely to shop there repeatedly.
To know more about veterinary practice:
https://brainly.com/question/27817241
#SPJ11
Use the rational zeros theorem to find all the real zeros of the polynomial function. use the zeros to factor f over the real numbers. f(x)=x^3-5x^2-61x-55???
Answers
The polynomial function f(x) = x³ - 5x² - 61x - 55 has the following
Real zeros: x = -5, x = -1, and x = 11.
To find the rational zeros of a polynomial, we use the rational zeros theorem. We look at the factors of the leading coefficient and the factors of the constant coefficient.
The states that if a polynomial function is defined as P(x) = anxn + an-1xn-1 + ... + a1x + a0 with integers, then each rational zero of the polynomial can be expressed in the form p/q where p is a factor of a0 and q is a factor of an.
For example, if P(x) = 2x³ - 5x² + 3x + 6 then p can be any factor of 6 and q can be any factor of 2.
The factors of the leading coefficient, 1, and the factors of the constant coefficient, -55, are: ±1, ±5, ±11, ±55. So the possible rational zeros are: ±1, ±5, ±11, ±55, ±1/1, ±5/1, ±11/1, ±55/1, ±1/1, ±5/1, ±11/1, ±55/1.
Simplifying the results, we have that the potential rational zeros are: ±1, ±5, ±11, ±55, ±1, ±5, ±11, and ±55.
By testing each possible rational zero, we find that x = -5, x = -1, and x = 11 are the real zeros of f(x).
Hence, using synthetic division, we get:
(x + 5)(x + 1)(x - 11) = x³ - 5x² - 61x - 55
Thus, the function can be factored over the real numbers as
f(x) = (x + 5)(x + 1)(x - 11).
To learn more about Rational Zero Theorem: https://brainly.com/question/31070385
#SPJ11
The value of y varies directly with x
Answers
The calculated value of y when x is -4 is -10 given that the variation is a direct variation
Calculating the value of y when x is -4Direct variation is a mathematical concept that describes the relationship between two variables that change in proportion to each other.
More formally, two variables x and y are said to vary directly if their ratio is constant. This can be expressed mathematically as:
y = kx
So, we have
20 = -8k
This gives
k = -2.5
This means that
y = -2.5x
When the value of x is -4 we have
y = -2.5 * -4
Evaluate
y = 10
Hence, the value of y when x is -4 is -10
Read more about direct variation at
https://brainly.com/question/6499629
#SPJ1
Given that a function, h, has a domain of -3 ≤ x ≤ 11 and a range of 1 ≤ h(x) ≤ 25 and that h(8) = 19 and h(-2) = 2, select the statement that could be true for h.
A. h(-3) = -1
B. h(13) = 18
C. h(2) = 16
D. h(8) = 21
Answers
The statement that could be true for h for given function is Option C h(2) = 16 is correct.
What is Domain?The set of all potential values for the independent variable (typically designated as x) for which the function is specified is known as the domain of a function. In other terms, it refers to the entire set of input values for which a function returns a result.
We can state that for any value of x between -3 and 11, the corresponding value of h(x) will be between 1 and 25 because the function h has a domain of -3 x 11 and a range of 1 h(x) 25.
Indicates that the function h is not fixed and that its values change depending on the value of x.
Now, evaluate your options:
Option A h(-3) = -1 - This statement is false because the range of h(x) is stated to be between 1 and 25, so h(-3) cannot be less than 1.
OptionB h(13) = 18 - This statement cannot be true because h(x) is specified to have a range between -3 and 11, so h(13) is not defined.
OptionC h(2) = 16 - The statement may be accurate given that the value of h(x) for any x between -3 and 11 could range from 1 to 25, and there is no evidence to the contrary.
OptionD h(8) = 21 - Since we know that h(8) = 19, this assertion is false.
Therefore, the statement that could be true for h is: h(2) = 16
To learn more about Domain
https://brainly.com/question/29452843
#SPJ9
how could you lower the fat content of the following sandwich? 2 slices of white bread 2 ounces of sliced turkey 1 slice of provolone cheese 1 tablespoon of mayonnaise 1 leaf of lettuce 1 slice of tomato
Answers
1. Replace the white bread with whole grain bread
2. Replace the turkey with a leaner meat, such as chicken or turkey bacon
3. Replace the mayonnaise with low-fat Greek yogurt
4. Replace the provolone cheese with a lower-fat cheese such as mozzarella
5. Reduce the amount of lettuce used
6. Replace the tomato slice with tomato slices or tomato paste.
To lower the fat content of the sandwich, you can make these changes:
Learn more about turkey
brainly.com/question/801345
#SPJ11
A ball is thrown from an initial height of 3 meters with an initial upward velocity of 30(m)/(s). The ball's height h (in meters) after t seconds is given by the following.
h=3+30t-5t^(2)
Find all values of t for which the ball's height is 13 meters.
Answers
Answer: -451
Step-by-step explanation:
so, the height we are trying to find is 13 meters.
13=3+30t-5t^2
so, we can go ahead and pull that number in.
now we have to subtract the 3 to try and get as much as possible over on the other side to find t.
10=30t-5t^2
Step-by-step explanation:
h(t) = 3 + 30t - 5t²
the height is set to 13 meters.
since the ball will go up and then come back down again, we expect 2 points of time, when the ball is at 13 meters high. if any at all, by the way (keep that in mind for similar questions, the object might not even reach a certain height).
13 = 3 + 30t - 5t²
10 = 30t - 5t²
2 = 6t - t²
0 = -t² + 6t - 2
the general solution to a quadratic equation
ax² + bx + c = 0
is
x = (-b ±sqrt(b² - 4ac))/(2a)
in our case
x = t
a = -1
b = 6
c = -2
t = (-6 ±sqrt(6² - 4×-1×-2))/(2×-1) =
= (-6 ±sqrt(36 - 8))/-2 = (-6 ±sqrt(28))/-2 =
= (-6 ±sqrt(4×7))/-2 = (-6 ±2×sqrt(7))/-2 =
= 3 ± sqrt(7)
t1 = 3 + sqrt(7) = 5.645751311... seconds
t2 = 3 - sqrt(7) = 0.354248689... seconds
on its way up the ball will pass the mark of 13 meters after about 0.35 seconds, and on its way back down it will pass the mark of 13 meters again after about 5.65 seconds.
you are placing 11 different pictures on separate pages of a photo album. how many different ways can you order the 11 pictures in the album?
Answers
The number of different ways to order 11 different pictures in a photo album is 39,916,800.
To calculate this number, we can use the formula for permutations, which is:
n! / (n - r)!
where n is the total number of items to choose from (in this case, 11 pictures) and r is the number of items to be selected (also 11, since we want to order all the pictures).
Plugging in the values, we get:
11! / (11 - 11)! = 11! / 0! = 11!
We can simplify 11! as:
11! = 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
Using a calculator or by hand, we can find that 11! equals 39,916,800.
Therefore, there are 39,916,800 different ways to order 11 different pictures in a photo album.
Hence, the number of ways to order 11 pictures in a photo album can be calculated using the permutation formula, which gives a total of 39,916,800 possible arrangements.
To know more about permutations, refer here:
https://brainly.com/question/30649574#
#SPJ11
HELP NOW!
Without graphing, identify the key features of the given function.
-vertex
-axis of symmetry
-direction of opening
-number of x-intercepts
-compression/expansion
[tex]f(x)=2(x-3)^2+5[/tex]
Explain your answers on how you found each answer.
Answers
The key features of the given function include the following:
Vertex = (3, 5)
Axis of symmetry = 3.
Direction of opening: upward.
Number of x-intercepts = 0.
Expansion.
What is the vertex form of a quadratic equation?In this exercise, you are required to determine the vertex form of a quadratic function h(x) that is written in standard form. Mathematically, the vertex form of a quadratic equation is given by this formula:
y = a(x - h)² + k
Where:
h and k represents the vertex of the graph.a represents the leading coefficient.Based on the information provided about this quadratic function, we can reasonably infer and logically deduce that its vertex can be determined as follows:
y = a(x - h)² + k
f(x) = 2(x - 3)² + 5
Vertex, (h, k) = (3, 5)
Axis of symmetry, Xmax = -b/2a = -(-6)/2(1) = 6/2 = 3.
In conclusion, the function does not have an x-intercept and it represents an expansion because the scale factor is greater than one (1) i.e k = 2.
Read more on vertex here: brainly.com/question/14946018
#SPJ1
Parker Paint has just created a new color, Sunset Orange, made by mixing 3 parts of Fire Red with 5 parts of Brilliant Yellow. A graph to help customers decide how much paint they need is hanging in the store. Use the point shown from the graph to help you decide how much Fire Red paint is needed to paint one 8 foot by 10 foot wall.
Answers
To paint an 8 foot by 10 foot wall with Sunset Orange, one needs 48 parts of Fire Red and 80 parts of Brilliant Yellow.Using the graph, we can calculate that for every 5 parts of Brilliant Yellow, 3 parts of Fire Red is needed.
Using the graph, we can calculate that for every 5 parts of Brilliant Yellow, 3 parts of Fire Red is needed. Since we need to paint an 8 foot by 10 foot wall, we need 80 square feet of paint. To calculate how much Fire Red is needed, we can use the equation: 3 parts of Fire Red = 5 parts of Brilliant Yellow. We can rearrange this equation to read: 5 parts of Brilliant Yellow = 3 parts of Fire Red. To get the amount of Fire Red required to paint the wall, we can multiply 80 (the square footage of the wall) by 3 and divide it by 5, giving us a total of 48 parts of Fire Red.
To paint an 8 foot by 10 foot wall with Sunset Orange, one needs 48 parts of Fire Red and 80 parts of Brilliant Yellow.
Learn more about graph here
https://brainly.com/question/17267403
#SPJ1
The pseudoinverse of the null (all zero) vector is the transposed null vector. The pseudoinverse of a non-nullvector is the conjugate transposed vector divided by its squared magnitude:x+ = { 0,. if x = 0;x-1 otherwise.
Answers
What is a pseudoinverse?
The pseudoinverse of the null (all zero) vector is indeed the transposed null vector. This is because the null vector has no direction or magnitude, so when we calculate its pseudoinverse, we are essentially looking for a vector that when multiplied with the null vector gives us the identity matrix. Since there is no such vector, the pseudoinverse is simply the transposed null vector.However, for a non-null vector, the pseudoinverse is calculated using a different formula. Specifically, the pseudoinverse of a non-null vector x is given by the conjugate transposed vector divided by its squared magnitude.
This is denoted by x+ and is defined as follows:
x+ = {0, if x = 0; x*-/(||x||^2), otherwise.
Here, x* denotes the conjugate transpose of x, and ||x||^2 represents the squared magnitude of x. Essentially, we are finding a vector that when multiplied with x gives us the identity matrix (or as close to it as possible). This vector is the pseudoinverse, and it is computed using the formula above.
So in summary, the pseudoinverse of the null vector is the transposed null vector, while the pseudoinverse of a non-null vector is the conjugate transposed vector divided by its squared magnitude.
To learn more about ''The pseudoinverse of the null (all zero) vector'' visit : https://brainly.com/question/15297129
#SPJ11
two cyclists, 48 mi apart, start riding towards each other at the same time. one cycles twice as fast as the other. if they meet 1 hr later, at what average speed is each cyclist traveling?
Answers
The slower cyclist travels at a speed of 16 miles per hour, while the faster cyclist travels at twice the speed, which is 32 miles per hour.
Let's assume that the slower cyclist's speed is x mi/h, then the faster cyclist's speed is 2x mi/h.
Since they are riding towards each other, their relative speed is the sum of their speeds, which is 3x mi/h.
They travel a total distance of 48 mi in 1 hour, so we can use the formula:
distance = rate x time
48 = 3x x 1
Solving for x, we get:
x = 16
Therefore, the slower cyclist's speed is 16 mi/h and the faster cyclist's speed is 32 mi/h.
Learn more about Speed here:
https://brainly.com/question/28748114
#SPJ4
Help please hurry
Maria spins a penny 100 times and it lands head side up 62 times. Explain why Maria's experimental probability may be different from the theoretical probability of spinning a coin. (10 points)
Answers
Answer:
To solve the question we shall proceed as follows:
Theoretical probabilities generally deals with the nature of the experiment and events, this differs from the experimental probabilities relies on the fact of actual occurrence of the experiment and the events. In other words, experimental probability is an estimate simply based on the probabilities that cannot at all be determined by simple logic. It is the ratio of the number of times an event is occurring to the total number of times or trials that an activity has been repeated for.
From the question, the experimental probability will be:
62/100
=0.62
this differs with theoretical probability which states that at any occasion the probability of the coin coming up heads when tossed is 1/2
Step-by-step explanation: I really hope this helps!! :))). Mark me brainliest!! :))
What is the volume of a sphere with a radius of 60.5ft
Answers
Answer: V ≈ 927,587
Step-by-step explanation:
Formula for volume of a sphere:
V = [tex]\frac{4}{3}[/tex]πr³
Substitute the known value for radius:
V = [tex]\frac{4}{3}[/tex]π(60.5ft)³
Simplify:
V ≈ 927,587
How do I work this out
Answers
Therefore, the equation of the line is y = 6x + 1, in slope-intercept form.
What is equation?In mathematics, an equation is a statement that shows the equality of two expressions. An equation usually contains one or more variables, which represent unknown values that we are trying to solve for. Equations can also be more complex, involving multiple variables and operations such as exponents, logarithms, and trigonometric functions. Solving equations is an important part of mathematics, and has many practical applications in science, engineering, and everyday life.
Here,
The equation of a straight line in slope-intercept form is y = mx + b, where m is the gradient (or slope) of the line, and b is the y-intercept (where the line crosses the y-axis). We are given that the gradient of the line is 6, and that it passes through the point (3, 19). We can use this information to find the equation of the line. First, we can use the point-slope form of the equation of a line to find the equation of the line that passes through the point (3, 19) with a gradient of 6. The point-slope form is:
y - y1 = m(x - x1)
where (x1, y1) is the point the line passes through, and m is the slope of the line.
Substituting the values we know, we get:
y - 19 = 6(x - 3)
Expanding the brackets, we get:
y - 19 = 6x - 18
Adding 19 to both sides, we get:
y = 6x + 1
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
Solve:
6n-5=-35
R=12=25
9x+3=21
Answers
Answer:
6n - 5 = -35
Adding 5 on both sides, we get
6n = -30
Dividing by 6 on both sides, we get
n = -5
R/12 = 25
Multiplying both sides by 12, we get
R = 300
9x + 3 = 21
Subtracting 3 from both sides, we get
9x = 18
Dividing by 9 on both sides, we get
x = 2
use the properties of geometric series to find the sum of the series. for what values of the variable does the series converge to this sum?
7−14z+28z2−56z3+⋯
sum =
domain =
(Give your domain as an interval or comma separated list of intervals; for example, to enter the region x<−1 and 2
Answers
a) The sum of the given series is 7 / (1 + 2z)
b) The domain of convergence is (-∞, -1/2) U (1/2, ∞).
The given series can be expressed as
7 – 14z + 28z^2 - 56z^3 + ...
This is a geometric series with first term (a) = 7 and common ratio (r) = -2z. The formula for the sum of an infinite geometric series is
sum = a / (1 - r)
Substituting the values of a and r, we get
sum = 7 / (1 + 2z)
So, the sum of the given series is 7 / (1 + 2z).
For the series to converge, the absolute value of the common ratio must be less than 1. That is,
|r| = |−2z| < 1
Simplifying this inequality, we get
1/2 < |z|
So, the domain of convergence of the given series is (-∞, -1/2) U (1/2, ∞).
Learn more about infinite geometric series here
brainly.com/question/28585723
#SPJ4
If g(x) = 1 – 2x + 3x2, find the average rate of change of the function as x varies from 2 to 5
Answers
The average rate of change of the function as x varies from 2 to 5 is 22.
Given function: g(x) = 1 – 2x + [tex]3x^2[/tex]
To find the average rate of change of the function as x varies from 2 to 5.
Solution: We are given a function: g(x) = 1 – 2x + [tex]3x^2[/tex]
The average rate of change of the function as x varies from a to b is given by:
Average rate of change = f(b) - f(a) / b - a
Let a = 2 and b = 5
We have to find the average rate of change of g(x) as x varies from 2 to 5.
So, the average rate of change of g(x) is given by:
Average rate of change = g(5) - g(2) / 5 - 2
= [1 - 2(5) + 3([tex]5^2[/tex])] - [1 - 2(2) + 3([tex]2^2[/tex])] / 3
= [1 - 10 + 75] - [1 - 4 + 12] / 3= 66 / 3= 22
Therefore, the average rate of change of the function as x varies from 2 to 5 is 22.
An average rate of change is the amount that the function changes on average over a specified interval.
The formula for average rate of change is given as the change in the function value divided by the change in x value for two distinct points on the function.
For similar question on function.
https://brainly.com/question/22340031
#SPJ11
the probability that no cars will pass by a section in an hour is 0.4 (modelled as a poisson process. further, no car passed by in the last 2 hours. what is the probability that you have to wait at least 1 more hour (after the 2 hours) for the next car?
Answers
The probability of having to wait at least 1 more hour for the next car is 0.631 or approximately 63.1%.
The given problem can be solved using the Poisson distribution. Let [tex]$\lambda$[/tex] be the average rate of cars passing through the section per hour. Then, since the probability of no cars passing in one hour is 0.4, we have:
[tex]$P(X=0)=\frac{\lambda^0e^{-\lambda}}{0!}=0.4$[/tex]Solving for [tex]$\lambda$[/tex], we get [tex]$\lambda= -ln(0.4) \approx 0.916$[/tex]. Therefore, the probability of no cars passing in three hours (two hours have already passed) is:
[tex]$P(X=0 \text{ in } 3 \text{ hours})=\frac{(0.916\cdot3)^0e^{-0.916\cdot3}}{0!} \approx 0.148$[/tex]The probability of waiting at least 1 more hour for the next car is the same as the probability of having no cars pass in the next hour, given that no cars have passed in the last 2 hours. This can be calculated using the conditional Poisson distribution:
[tex]$P(X=0 \text{ in } 1 \text{ hour} | X=0 \text{ in } 3 \text{ hours}) = \frac{P(X=0 \text{ in } 1 \text{ hour and } X=0 \text{ in } 3 \text{ hours})}{P(X=0 \text{ in } 3 \text{ hours})}$[/tex][tex]$= \frac{\frac{(0.916\cdot1)^0e^{-0.916\cdot1}}{0!}\cdot \frac{(0.916\cdot2)^0e^{-0.916\cdot2}}{0!}}{0.148} \approx 0.631$[/tex]
Therefore, the probability of having to wait at least 1 more hour for the next car is 0.631 or approximately 63.1%.
Learn more about Probability:
https://brainly.com/question/24756209
#SPJ4
WILL GIVE BRIANLIST TO BEST ASNWWR
Richard buys a new car for $28,000. The car depreciates in value by 9% each year. Which of the following uses the variable y to represent the value of the car after t years in an exponential model to represent the situation?
y=28,000(1.09)
y=28,000(91)
y-28,000(-9)
y=28,000(0.09)
Answers
The variable y is used to represent the worth of the car after t years like an exponential model to reflect the scenario, and the third option, y=28,000(0.91)t, is the correct response.
The formula for the exponential model is what?A = A0(b)t/c is the formula for an exponential model, where A0 denotes the starting quantity of the thing being modeled. t stands for passing time. The quantity at time t is equal to A.
The exponentially decaying formula for an asset's value over time with such a consistent rate of depreciation is: y = a(1-r)t
Where:
Y is equal to the car's value after t years.
In this scenario, the car's original value is $28,000, and its rate of depreciation is 9%, or 0.09 in decimal notation.
t equals the amount of years
The exponential model can be expressed using the following formula: y = 28,000(1-0.09)t
By condensing the formula, we obtain the following result: y = 28,000(0.91)t
To know more exponential model visit:
https://brainly.com/question/28596571
#SPJ1
how do u sovle Find x .
Two non-congruent parallelograms. The width and length of one parallelogram are marked 4 centimeters and 6 centimeters respectively. The width and length of the other parallelogram are marked 6 centimeters and x respectively.
Answers
The length of the second parallelogram is 2 cm.
What are parallelograms ?
A parallelogram is a quadrilateral with opposite sides parallel and equal in length. It has two pairs of parallel sides and opposite angles are equal. Some common properties of parallelograms include:
According to the question:
To solve for x, we need to use the fact that opposite sides of a parallelogram are equal in length.
For the first parallelogram, we know that the width is 4 cm and the length is 6 cm. Therefore, the opposite side lengths are also 4 cm and 6 cm.
For the second parallelogram, we know that the width is 6 cm. Since the opposite sides are equal in length, the length of the parallelogram must be x cm.
So, we have:
Width of first parallelogram = Width of second parallelogram
4 cm = 6 cm
Length of first parallelogram = Length of second parallelogram
6 cm = x cm
Simplifying the first equation, we get:
2 cm = x
Therefore, the length of the second parallelogram is 2 cm.
To know more about parallelograms visit:
https://brainly.com/question/28854514
#SPJ1
Find the area of the following shapes. Please help
A=?cm2
Answers
The shape is an identical parallelogram and the area is equal to 30 square centimeters.
Area of parallelogramIn calculating for the area of parallelogram, the base is multiplied by the height, as the same way for calculating the area of a rectangle.
we shall calculate for the area of the shape by evaluating the area of the one parallelogram and then multiply the result by two as follows:
area of one identical parallelogram = 5 cm × 3 cm
area of one identical parallelogram = 15 cm²
area of identical parallelogram shape = 2 × 15 cm²
area of identical parallelogram shape = 30 cm²
Therefore, the area for the identical parallelogram shape is equal to 30 square centimetres.
Know more area of parallelogram here: https://brainly.com/question/970600
#SPJ1
the sides of a square are growing at a rate of 3 inches per minute. how fast is the area increasing when each side is 5 inches long?
Answers
24 centimeters. Hope this helped!
There are 35 counters in a bag the ratio of red to blue counters is 2:5 there are 9 more blue counters the rest are green how many green counters are there?
Answers
there are 6 red counters, 24 blue counters, and 5 green counters in the bag, based on the given information. The given information provides us with the ratio of red to blue counters in a bag, which is 2:5. This means that for every 2 red counters in the bag, there are 5 blue counters.
Let the number of red counters in the bag be 2x, where x is a constant. Then, the number of blue counters in the bag is 5x. We are also given that there are 9 more blue counters than before, so the new number of blue counters is 5x + 9.
We know that there are 35 counters in total, so we can write an equation based on this information:
2x + 5x + 5x + 9 = 35
Simplifying this equation, we get:
12x + 9 = 35
Subtracting 9 from both sides, we get:
12x = 26
Dividing both sides by 12, we get:
x = 2.1667
Since we cannot have a fraction of a counter, we can round x up to 3.
Therefore, the number of red counters in the bag is 2x = 2(3) = 6, and the number of blue counters in the bag is 5x + 9 = 5(3) + 9 = 24.
Finally, we can find the number of green counters in the bag by subtracting the number of red and blue counters from the total number of counters:
35 - 6 - 24 = 5
So there are 5 green counters in the bag.
In summary, there are 6 red counters, 24 blue counters, and 5 green counters in the bag, based on the given information.
To know more about ratio click here:
brainly.com/question/13419413
#SPJ4
Kevin is hiking on a trail that is 4. 9 miles long. So far, he has hiked 90% of the total distance. How many more miles does Kevin have to hike in order to complete the trail? Complete the explanation on how you found your answer. Part 1 out of 2 Kevin has to hike more miles in order to complete the trail
Answers
Kevin has 0.49 miles, or approximately 0.5 miles, left to hike in order to complete the trail.
Kevin has hiked 90% of the trail, which means he still has to hike 10% of the trail to complete it. To find out how many miles he has left to hike, we can use the proportion:
10/100 = x/4.9
where x represents the number of miles Kevin has left to hike.
To solve for x, we can cross-multiply and simplify:
10 * 4.9 = 100x
49 = 100x
x = 49/100
x = 0.49
Therefore, Kevin has 0.49 miles, or approximately 0.5 miles, left to hike in order to complete the trail.
Learn more about Distance:
https://brainly.com/question/28551043
#SPJ4
Complete Question:
Kevin is hiking on a trail that is 4. 9 miles long. So far, he has hiked 90% of the total distance. How many more miles does Kevin have to hike in order to complete the trail?
10. Which graph shows the solution to the inequality <-6?
Answers
eighteen more than 7 times a number is -12
Answers
The solution x = -30/7 is the value of the unknown number that satisfies the statement "eighteen more than 7 times a number is -12".
This question is incomplete, the complete question is:
Eighteen more than 7 times a number is -12, find the unknown number.
What is the value of the unknown number?Given that, eighteen more than 7 times a number is -12.
Let's use "x" to represent the unknown number.
From the given information, we can use algebra to translate this sentence into an equation.
We start by using "7x" to represent the product of 7 times "x", and adding 18 to it:
7x + 18
Then, we set this expression equal to -12, since that's what the sentence told us the expression is equal to:
7x + 18 = -12
To solve for "x", we can first subtract 18 from both sides:
7x + 18 - 18 = -12 - 18
7x = -30
Then, we can isolate "x" by dividing both sides by 7:
7x/7 = -30/7
x = -30/7
Therefore, the value of the unknown number is x = -30/7.
Learn to solve more equations here: https://brainly.com/question/9236233
#SPJ1
Pls just say a b c or d
Answers
The prοbabiIity οf the spinner stοpping at green and a yeIIοw card being seIected is 1/18.
What is PrοbabiIity?PrοbabiIity is a measure οf the IikeIihοοd οf an event οccurring, expressed as a number between 0 and 1. It is caIcuIated as the number οf favοrabIe οutcοmes divided by the tοtaI number οf pοssibIe οutcοmes.
The prοbabiIity οf the spinner stοpping at green is 1/3 since there are three equaI parts.
The prοbabiIity οf seIecting a yeIIοw card frοm the six cards is 1/6 since there is οne yeIIοw card οut οf six cards in tοtaI.
Tο find the prοbabiIity οf bοth events happening, we muItipIy the individuaI prοbabiIities:
P(green and yeIIοw) = P(green) * P(yeIIοw)
= (1/3) * (1/6)
= 1/18
Therefοre, the prοbabiIity οf the spinner stοpping at green and a yeIIοw card being seIected is 1/18.
Tο learn more about Probability from the given link
https://brainly.com/question/24756209
#SPJ1
HELP 20 POINTS
NO WRONG ANSWERS OF LINKS THEY WILL GET REPORTED
Answers
Answer:
The second one, (x+1)(3x+2)
The answer is (x+1)(3x+2)
hope it helps
How will the product of 7 x
Choose 1 answer:
64
5
compare to 7, and why?
It will be less because we are multiplying 7 by a fraction that is less
than 1.
It will be equal because we are multiplying 7 by a fraction that is
equal to 1.
It will be greater because we are multiplying 7 by a fraction that is
greater than 1.
Answers
According to the question the product of 7 x 5 will be greater than 7 from multiplication.
Explain Multiplication?Multiplication in mathematics is the addition of equal groups. As we proliferate, the quantity of items in the group increases. The product as well as the two elements are part of a multiplication issue. 6 and 9 are factors in the multiplication equation 6 9 = 54, and 54 is the result.
The product of 7 x 5 by multiplying with each other we can get 35
The number being multiplied with 7 is greater than 1 so the product will also be greater than 7.
The product of 7 x 5 will be greater than 7 because we are multiplying 7 by a number greater than 1.
To know more about multiplication visits:
https://brainly.com/question/29793687
#SPJ1
Please help me I need this